Disjunktni skupovi implementirani preko povezane liste

Struktura podataka disjunktnih skupova održava kolekciju \(\mathcal{S} = \{ S_1, S_2, \ldots, S_k \}\) disjunktnih dinamičkih skupova. Svaki skup se identifikuje nekim svojim elementom, koga nazivamo predstavnik. Neka \(x\) i \(y\) označava neke objekate, želimo da struktura disjunktnih skupova podržava sledeće operacije:

Koristeći povezane liste implementirati strukturu disjunktnih skupova koja podržava sve tri operacije. Analizirati složenost svake operacije.

Opis ulaza

Opis izlaza

Rešenje

Opis glavnog rešenja

Na slici ispod, u prvom redu, ilustrovan je način implementiranja strukture disjunktnih skupova. Svaki skup je predstavljen sopstvenom povezanom listom. Svaki skup ima atribute: \(head\) koji pokazuje na prvi objekat u listi; i \(tail\) koji pokazuje na poslednji objekat u listi. Svaki objekat u povezanoj listi sadrži element skupa, pokazivač na sledeći objekat u listi, i pokazivač na skup kome pripada. Unutar povezane liste objekti nisu uređeni. Predstavnik skupa je prvi objekat u listi.

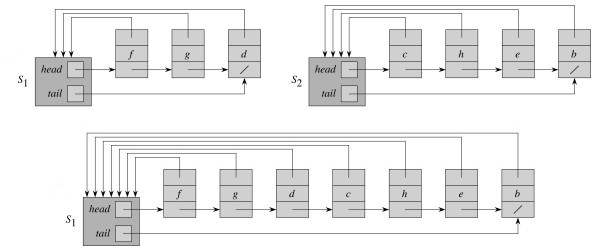
Operaciju \(make\_set(x)\) možemo implementirati jednostavno tako što napravimo novu povezanu listu koja sadrži samo objekat \(x\). Operaciju \(find\_set(x)\), takođe, implementiramo jednostavno tako što pratimo pokazivač na skup kome \(x\) pripada i vratimo element na koji \(head\) pokazuje. Obe operacije \(make\_set(x)\) i \(find\_set(x)\) su konstantne vremenske složenosti. Operacija \(union(x, y)\) zahteva da se lista kojoj \(y\) pripada nadoveže na kraj liste kojoj \(x\) pripada (na slici gore, u drugom redu je prikazana unija skupa \(S_1\) i \(S_2\)). Ovo možemo izvršiti u konstantnoj vremenskoj složenosti, kako imamo pokazivače na prvi i poslednji element liste. Međutim, potrebno je ažurirati pokazivač na skup svih elemenata povezane liste kojoj \(y\) pripada. Zbog toga je amortizovana složenost operacije unije \(\Theta(n)\), gde je \(n\) ukupan broj elemenata.

Ovaj pristup implementiranja strukture disjunktnih skupova je naivan. Pored njega, postoji još jedan naivan način za implementiranje disjunktnih skupova preko niza/mape. Bolje rešenje se dobija kada strukturu disjunktnih skupova implementiramo preko disjunktne šume, zajedno sa dve heuristike: unija po rangu i kompresija putanje. Za više detalja pogledati knjigu.

#include <iostream>
#include <vector>

using namespace std;

int ID = 0;

struct set;

struct element {
    char id;
    struct set *set = nullptr;
    struct element *next = nullptr;
};

struct set {
    int id;
    struct element *head = nullptr;
    struct element *tail = nullptr;
};

void make_set(struct element *x) 
{
    auto new_set = new set();

    new_set->id = ID++;
    new_set->head = x;

    x->set = new_set;
}

struct element *find_set(struct element *x) 
{
    return x->set->head;
}

void union_set(struct element *x, struct element *y)
{
    auto x_set = find_set(x)->set;
    auto y_set = find_set(y)->set;

    x_set->tail->next = y_set->head;
    x_set->tail = y_set->tail;

    auto y_head = y_set->head;
    while (y_head != nullptr) {
        y_head->set = x_set;
        y_head = y_head->next;
    }
}

void print_element(struct element *x)
{
    cout << x->id << " ";
}

void print_set(struct set *s)
{
    cout << s->id << " [ ";
    auto head = s->head;
    while (head != nullptr) {
        print_element(head);
        head = head->next;
    }
    cout << "]" << endl;
}

int main(void)
{
    auto a = new element(); a->id = 'a';
    auto b = new element(); b->id = 'b';
    auto c = new element(); c->id = 'c';
    auto d = new element(); d->id = 'd';
    auto e = new element(); e->id = 'e';
    auto f = new element(); f->id = 'f';
    auto g = new element(); g->id = 'g';

    make_set(a);
    make_set(b);
    make_set(c);
    make_set(d);
    make_set(e);
    make_set(f);
    make_set(g);

    union_set(a, b);
    union_set(a, c);
    union_set(d, e);
    union_set(d, f);
    union_set(d, g);

    print_set(a->set);
    print_set(f->set);

    union_set(a, f);

    print_set(a->set);

    delete find_set(a);

    delete a;
    delete b;
    delete c;
    delete d;
    delete e;
    delete f;
    delete g;

    return 0;
}